Árboles filogenéticos

¿Conocéis el chiste aquel de los dos presos que hace mucho tiempo que comparten celda, y va uno y le pide al otro “Va, cuéntame un chiste”, el otro contesta “El 56” y el primero se parte de risa? Pues últimamente yo estoy en la tesitura de “Va, dame un árbol”, y ya me va bien que me den el 56, pero claro, luego he de saber cuál es. En última instancia, numerar objetos es una manera de ponerles nombre y por lo tanto de poseerlos. Pero entonces es necesario un diccionario que nos permita recuperar los objetos a partir de los números, y si ese diccionario se puede reducir a un algoritmo sencillo, mejor.

En el caso de los árboles (en lo que sigue, por un “árbol” entiendo un árbol en el sentido de la teoría de grafos y con raíz, que en los dibujos corresponde al nodo superior), hay una numeración muy útil: los números de Matula, que se definen recursivamente de la manera siguiente. Si $T$ es un árbol de un solo nodo, $M(T)=1$ . Si $T$ tiene más de un nodo y $T_1,\ldots,T_k$ son los subárboles que cuelgan de los hijos de su raíz y $m_1=M(T_1),\ldots, m_k=M(T_k)$ son los números de Matula de estos subárboles y $p_{m_1},\ldots,p_{m_k}$ son los primos $m_1$ -ésimo, $m_2$ -ésimo, …, $m_k$ -ésimo, entonces $M(T)=p_{m_1}\cdots p_{m_k}$ .

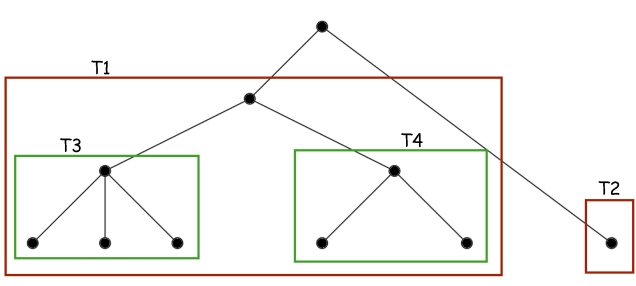
Veamos un ejemplo. Considerad el árbol de la figura, lo llamaremos T (y como hoy es el día del orgullo friki, uso Comic Sans).

Para calcular su número de Matula, hemos de calcular los de sus subárboles T1 y T2. El de T2 és fácil: 1, porque es un solo nodo (una hoja). El número de Matula de T1 será el producto de los primos correspondientes a los de T3 y T4, así que necesitamos calcular primero los números de Matula de T3 y T4. Veamos: la raíz de T3 tiene 3 hijos y los tres son hojas, por lo que cada uno define un subárbol de un solo nodo; por lo tanto, cada uno de estos subárboles tiene número de Matula 1, y como el primer primo es $p_1=2$ , tenemos que $M(T3)=p_1\cdot p_1\cdot p_1=2\cdot 2 \cdot 2=8$ . Por otro lado, la raíz de T4 tiene 2 hijos, los dos hojas, por lo que cada uno define un subárbol de un solo nodo, de número de Matula 1. Obtenemos entonces que $M(T4)=p_1\cdot p_1=2\cdot 2=4$ .

Como T3 y T4 son los árboles número 8 y 4, respectivamente, por la recurrencia, $M(T1)$ será el producto del octavo primo, $p_{8}=19$ , y del cuarto primo, $p_4=7$ : $M(T_2)=19\cdot 7=133$ . Y como $M(T2)=1$ , tenemos finalmente que $M(T)$ será el producto del primo en la posición 133, $p_{133}=751$ y del primer primo, $p_1=2$ . Es decir, $M(T)=751\cdot 2=1502$ .

Este proceso se puede invertir. Dado un número $N$ , lo descomponemos en producto de números primos $N=q_1\cdots q_m$ y buscamos cuál es el número de orden de cada $q_i$ en la lista de todos los primos: digamos que cada $q_i$ es el primo $m_i$ -ésimo. Entonces, la raíz de el árbol T $M(T)=N$ tendrá m hijos, y de ellos colgarán los árboles $T_i$ número $M(T_i)=m_i$ . Naturalmente, si $N=1$ entonces T es el árbol de un solo nodo, por definición.

Por ejemplo, ¿cuál el es árbol 2017? 2017 es primo, en concreto $p_{306}$ . Por lo tanto el árbol 2017 estará formado por una raíz de la que cuelga un solo hijo, que es la raíz del árbol número 306. Ahora $306=2\cdot 3\cdot 3 \cdot 17$ . Como $p_1=2$ , $p_2=3$ y $p_7=17$ , el árbol 306 está formado por una raíz de la que cuelgan 4 hijos, que son raíces de un árbol número 1 (un solo nodo), dos árboles número 2, y un árbol número 7. Os dejo terminar: el árbol número 2 está formado por una raíz con un único hijo que además es una hoja, y el árbol número 7 ( $=p_4$ ) está formado por una raíz con un único hijo del que cuelgan dos hijos que son hojas. El resultado es el de la figura que sigue.

Por lo tanto, cada árbol tiene su número y cada número (natural y a partir de 1) representa un único árbol. Ya los tenemos numerado. Pero además, muchas propiedades de un árbol se pueden obtener a partir de su número, sin tener que reconstruir el árbol. Por ejemplo, su número de hojas. Es fácil comprobar, siguiendo la reconstrucción de un árbol a partir de su número, que si llamamos $N(T)$ al número de hojas de T e indicamos por $T_n$ el árbol número $n$ , entonces

$N(T_1)=1$ ,
$N(T_n)=N(T_m)$ si $n=p_m$
$N(T_n)=N(T_{q_1})+\cdots+N(T_{q_k})$ si $n=q_1\cdots q_k$ y $k\geq 2$

Por ejemplo, el número de hojas de nuestro árbol T número 2017 es $N(T_{2017}) =N(T_{306}) =N(T_{2\cdot 3\cdot 3 \cdot 17}) =N(T_2)+2N(T_3)+N(T_{17})=N(T_2)+2N(T_2)+N(T_{7})=3N(T_2) +N(T_4)=3N(T_2) +2N(T_2)=5N(T_2)=5N(T_1)=5$

¡Bien!

Otros muchos índices de un árbol se pueden calcular de manera recursiva a partir de su número de Matula. De hecho, ya os podéis imaginar que todo lo que se pueda calcular recurrentemente de hijos a padres se podrá determinar a partir del número de Matula. Si os interesa, este artículo de E. Deutsch explica la manera de calcular una trentena de índices.

Esta entrada participa en la edición 8.4 del Carnaval de Matemáticas, cuyo blog anfitrión es matematicascercanas.

—”Hola, me llamo Cesc y no siempre leo los artículos que cito.”

—”Hola, Cesc. No estás solo, Cesc.”

M.V. Simkin y V.P. Roychowdhury estimaron que los científicos sólo leemos un 20% de los artículos que citamos. Para ser precisos, estimaron que alrededor de un 80% de las citas a artículos célebres provienen de copiar la referencia de una bibliografía anterior sin consultar el original. Para llegar a esa conclusión, modelaron matemáticamente cómo se generan y propagan las erratas en las citas, suponiendo que:

cuando copiamos una referencia del original cometemos erratas con una cierta probabilidad,
cuando copiamos una referencia de otra bibliografía que contiene una errata sin consultar el original, mantenemos la errata,
si la referencia “copiada” tiene una errata pero consultamos el original, la detectamos y la corregimos.

A continuación, analizaron con su modelo los errores en las citas de algunos artículos muy citados, y a partir de dicho análisis llegaron a ese porcentaje. Desde entonces han publicado varios artículos refinando su modelo (el último aquí) con conclusiones similares.

Mi caso caería dentro de los considerados por Simkin y Roychowdhury. En los últimos dos años he trabajado con algunos amigos en problemas relacionados con el equilibrio de árboles filogenéticos. Por un árbol filogenético aquí me refiero a un árbol con raíz y con sus hojas etiquetadas con especies. Un árbol filogenético representa entonces una hipotética historia evolutiva de las especies asociadas a sus hojas partiendo de un ancestro en común (la raíz): las aristas representan la descendencia directa por mutaciones, y la flecha del tiempo va en el sentido de la raíz a las hojas. La siguiente figura (copiada de aquí) muestra dos árboles filogenéticos alternativos para un mismo conjunto de especies: en estos árboles concretos, la raíz es el ápice inferior y por lo tanto el tiempo discurre de abajo a arriba.

Como la forma de un árbol filogenético concreto es un reflejo de las características del proceso evolutivo subyacente, hay un cierto interés en filogenética por cuantificar las propiedades de esta forma mediante índices. Unos de los más usados son los llamados índices de equilibrio (balance indices, en inglés), que miden la tendencia en un árbol a que sus nodos estén equilibrados en el sentido de que los “hijos” de cada nodo tengan el mismo número de hojas descendientes. En este sentido, los árboles que se consideran más “desequilibrados” son las orugas (con la forma del árbol de la derecha de la figura inferior; si en el Árbol I de la figura superior quitáis el cerdo, obtenéis un árbol oruga de 6 hojas).

Uno de los índices más usados en este contexto es el llamado índice de Sackin S, en honor a M. J. Sackin. Si definimos la profundidad de una hoja como el número de nodos interiores en el camino de la raíz a la hoja, contando la raíz, entonces el índice de Sackin de un árbol filogenético es la suma de las profundidades de todas sus hojas. Es un buen índice, fácil de entender y de calcular, con una buena correlación entre su magnitud y el equilibrio del árbol. De hecho, su desequilibrio: a mayor índice de Sackin, más desequilibrado es el árbol. Además, es igual a la suma de las hojas descendientes de cada nodo interior, y siempre es bonito tener dos expresiones sencillas de un mismo índice.

Por ejemplo, para los árboles de la figura anterior (y sumando profundidades de izquierda a derecha)

S(Tree I)=1+2+4+4+4+5+5=25, S(Tree II)=1+3+3+4+4+4+4=23

lo que indica que el árbol II está ligeramente más equilibrado que el I (gracias al cuarteto final, que en el árbol II define un subárbol simétrico).

La referencia obligada cuando se usa el índice de Sackin es

M. J. Sackin, “Good” and “bad” phenograms. Sys. Zool, 21 (1972), 225-226.

Pero claro, el índice de Sackin ya ha pasado a los libros de texto de filogenética, así que uno no va a buscar su formulación precisa en el artículo original, se fía de la referencia. Sobre todo si, como es mi caso, no se tiene acceso directo ni físico ni electrónico al texto completo del artículo de Sackin. Así, por ejemplo, J. Felsenstein en su “Inferring Phylogenies” (p. 563) dice que “Sackin (1972) sugirió usar o bien la varianza $\sigma_N^2$ de $N_i$ para la hojas del árbol o bien su media $\overline{N}$ , donde $N_i$ es el número de nodos en el árbol por debajo de la hoja i.”

Hace unas semana al fin encargué por intercambio bibliotecario una copia del artículo de Sackin y resulta que no, que Sackin no sugiere nada ni define ningún índice. En su artículo de dos páginas asocia a cada árbol el vector de las profundidades de sus hoja, demuestra que este vector caracteriza la forma de un árbol binario (donde cada nodo interior tiene exactamente dos hijos: los de las dos figuras lo son), y observa que, en los árboles de la siguiente figura (extraída de su artículo), el árbol simétrico de la izquierda tiene las profundidades de sus hojas más pequeñas y menos variadas que la oruga de la derecha. Y punto. Ningún índice explícito basado en estas profundidades, ninguna sugerencia de cuantificar el tamaño y la variación de estas profundidades.

¿Quién define pues el índice de Sackin? Hasta donde ha llegado mi búsqueda bibliográfica, la primera aparición del índice de Sackin es en el artículo sobre Tree Balance de K. T. Shao y R. R. Sokal en 1990 donde dicen (p. 266) “Sackin (1972) usó un vector b (de branching) para caracterizar un fenograma [un árbol filogenético binario] y medir su `utilidad'” y más adelante (p. 268) definen el “índice de Sackin” como lo hemos definido al principio. Por tanto, supongo que a partir de ahora para ser honrados citaremos (Sackin 1972, Shao-Sokal 1990).

Moraleja: no os fiéis de los libros de texto y las referencias celebres.

Ningún artículo citado en esta entrada ha sufrido el maltrato de no haber sido leído previamente.

Blioquinfo

Matemáticas, bioinformática y más

Árboles filogenéticos

¿Cuántas hojas tiene el árbol 2017?

Si no consultas, no cites